고정 헤더 영역
상세 컨텐츠
본문
2차원 벡터 v = (x, y) 일 때
이것을 Θ각 회전시키면
새로운 2차원 벡터 v2 = (xcosΘ - ysinΘ, xsinΘ + ycosΘ)가 된다.
(자세한 설명은 글 하단부에)
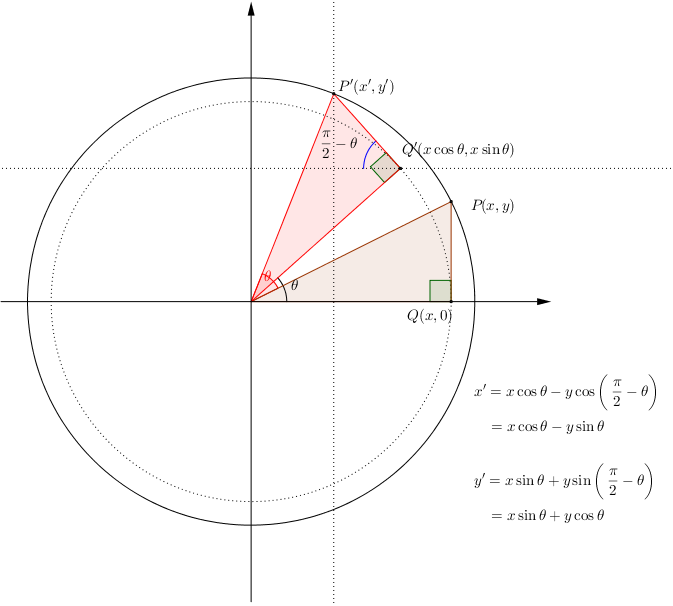
그러면 이제 회전 변환 공식을 추적해보자.
위에서 설정한 2차원 벡터 v = (x, y)를 2개의 벡터로 나눈다.
v = (x, 0) + (0, y)
vx = (x, 0)
vy = (0, y)
(벡터에 수를 곱하면 각 벡터의 요소(스칼라)에 그 수를 곱한다.)
그리고 vx, vy를 Θ만큼 돌린 후 두 벡터의 합을 구하면 회전 변환 공식이 완성된다.
(생각했던 것보다는 간단할 것이다.)
vx를 Θ만큼 돌리면 (x * cosΘ, x * sinΘ)
(vx의 길이가 x)
vy를 Θ만큼 돌리면 (y * sinΘ, y * cosΘ)
이렇게 나올 것 같지만 전혀 다르게 나온다.
(-y * sinΘ, y * cosΘ)
이렇게 나온다.
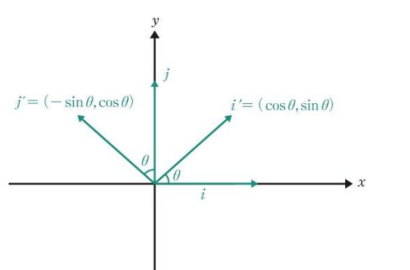
위의 그림은 기저 벡터를 회전시킨 것이다.
i = (1,0) , j = (0, 1) <- 이 귀여운 것들이 기저벡터이다
i'에 x를 곱하고
j'에 y를 곱한다.
그리고 x와 y를 곱한 두 벡터를 더한다!!
xi' + yj'
= (x * cosΘ, x * sinΘ) + (-y * sinΘ, y * cosΘ)
= (xcosΘ - ysinΘ, xsinΘ + ycosΘ)
그럼 우리가 구하고 싶었던 회전 변환 공식이 나오게 되는 것이다.
'게임 > 게임 수학' 카테고리의 다른 글
| 로그함수 f(x)가 같는 성질에 대한 함수 표현 (0) | 2020.04.02 |
|---|---|
| 수열의 합, 알아두면 쓸데없지만 편한 풀이 (0) | 2020.02.17 |
| 호도법 (7) | 2020.01.08 |





댓글 영역